기어에 대하여
기어
기어란
톱니바퀴 또는 기어(gear, 문화어: 기야)는 톱니의 맞물리는 힘으로 동력을 전달하는 장치이다. 간단한 단순 기계다. -Wikipedia
기어란 동력 전달 장치의 일종으로서, 그 중에서도 톱니의 맞물림을 통해 미끄러짐 없는 구름을 구현한 장치이다.
기어의 장점으로는 크게 (1) 미끄러짐 없는 구름운동이 가능, (2) 자유로운 가감속이 가능하다는 것이 있다.
기어의 종류
널리 사용하는 기어로는 스퍼 기어(평기어), 헬리컬 기어, 유성 기어, 베벨 기어, 웜 기어 등이 있으며 장단점을 파악하여 필요에 따라 사용하는 것이 유리하다.
스퍼 기어는 가장 사용하기 쉽다는 장점이 있다. 스퍼 기어는 평행한 두 축간 동력 전달밖에 하지 못한다.
헬리컬 기어는 스퍼 기어보다 소음이 적고 수명이 길다는 장점이 있으나, 가격이 비싸고 에너지 효율이 떨어진다는 단점이 있다.

헬리컬 기어
베벨 기어는 두 기어의 회전축을 교차해 놓은 형상을 가리킨다. 굳이 수직하게 교차할 필요 없이, 다양한 방향으로 조합이 가능하다. 베벨 기어에는 스퍼 기어 및 헬리컬 기어를 사용할 수 있다.

베벨 기어
웜 기어는 나선형의 웜과 스퍼(혹은 헬리컬) 기어 형상의 웜 휠을 맞물리게 하여 동력을 전달하는 장치이다. 웜이 회전하면 웜 휠이 돌지만, 웜 휠이 회전해서 웜을 돌릴 수는 없다.
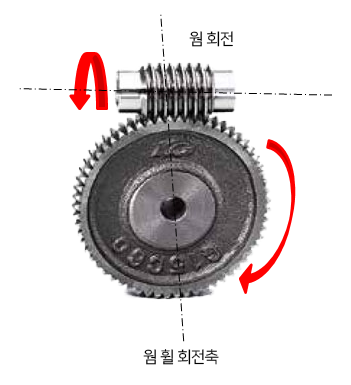
웜 기어
Fundamental law of gearing
기어는 “미끄러짐 없는 구름”을 구현하기 위한 장치인데, 이것은 적합한 설계를 통해서만 가능하다.
Fundamental law of gearing은 다음과 같다.
이 말을 다음과 같이 바꿔 쓸 수 있다.
아래의 조건을 성립하면 위의 조건을 성립한다. 자세한 내용은 Medium 글 섹션 5를 참고.
이때 pitch point로부터 기어 중심까지의 거리가 피치원 반지름이 된다. 피치원이란, 기어를 원기둥으로 모델링했을 때 기어의 둘레를 의미한다. 기어와 관련된 몇 가지 파라미터를 살펴보면 다음과 같다.
| 명칭 | 잇수(Number of teeth) | 피치원(Pitch diameter) | 지름피치(Diametral pitch) | 원주피치(Circular pitch) | 모듈(module) |
|---|---|---|---|---|---|
| 정의 | 기어의 총 이 개수 | 피치원의 지름 | 피치원 상에서 단위길이당 이 개수 | 피치원 상에서 이웃한 두 이 사이의 거리 | 원주피치 / pi |
| 식 | N | D | P = N/D | p = pi D/N | m = D/N |
Fundamental law of gearing을 만족하기 위해서는 P, p, m이 같은 기어들을 사용해야 한다.
기어 이(tooth) 형상
Fundamental law of gearing을 만족하는 대표적인 이 형상은 involute shape이다. Involute curve는 아래 사진과 같이 줄을 쭉 당겼을 때 만들어지는 곡선이다.
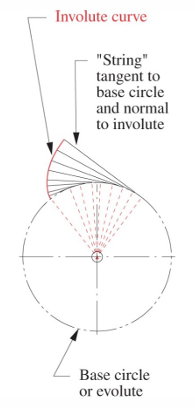
Involute shape 외에도 cycloidal shape을 사용할 수 있다.
기어비
기어비를 적절히 설정하면 원하는 만큼의 감속비를 얻을 수도 있고, 회전력을 증폭할 수도 있다.
위에서 모듈이 같은 기어끼리 사용해야 한다고 했는데, 이때 m을 고정하면 D 혹은 N을 자유롭게 조정할 수 있다. 보통은 N을 바꾸는데, 왜냐하면 N이 engineering parameter로서 의미가 있기 때문이다.
미끄러짐 없는 구름에서 두 기어가 맞닿는 지점에서의 선속도는 같다. 두 기어를 각각 1, 2라 하면 다음의 식이 성립한다.
\[v_1=v_2\]따라서 다음 식도 성립한다.
\[\omega_1 \frac {D_1}{2} = \omega_2 \frac {D_2}{2}\]모듈이 같다고 했으므로,
\[m_1 = \frac{D_1}{N_1} = \frac{D_2}{N_2} = m_2\]정리하면
\[\omega_2 = \frac{N_1}{N_2}\omega_1\]으로 기어 개수의 비(기어비)에 따라 회전속도가 바뀌는 것을 알 수 있다.
기어비를 조정하면 회전속도도 바뀌고 동시에 토크도 바뀐다. 에너지 보존 법칙을 생각해보면,
\[P_1 = \tau_1 \omega_1 = \tau_2 \omega_2 = P_2\]이므로 다음과 같이 토크가 증폭된다.
\[\tau_2 = \frac{N_2}{N_1}\tau_1\]정리하면,
\[\omega_2 = \frac{N_1}{N_2}\omega_1\\ \tau_2 = \frac{N_2}{N_1}\tau_1\]유성기어
특징
유성기어(Planetary gear set, Epicyclic gear)는 Sun gear 주변을 Planet gear가 돌고 이것을 Ring gear가 감싸고 있는 형태이다. 유성기어는 구동축과 회전축이 일치한다는 특성을 갖고 있다.
기어비
유성기어는 일반적으로 S, P, R 기어 중 하나를 고정시키고 하나를 구동하여 나머지 하나를 회전시킨다. 이때 감속비는 다음의 공식으로 계산할 수 있다.
\[\omega_S = -\frac{N_R}{N_S}\omega_R + (1+\frac{N_R}{N_S})\omega_P\]상황에 따라 \(\omega_S=0, \omega_R=0, \omega_P=0\)을 대입하여 계산하면 된다.
설계 예시
기어비 10 이상의 기어가 필요해서 만들기로함. 모터와 바퀴 사이에 달아야 하는데, 회전축을 달 공간이 마땅치 않아서 유성기어를 사용하기로 했다.
Ring gear가 지면과 접촉하는 바퀴의 역할을 할 것이고, sun gear가 모터와 연결된 구동축이 될 것이기 때문에 planet gear의 회전축을 고정하여야 한다\((\omega_P=0)\). 기어 잇수 및 모듈 선정은 다음의 Mixed integer nonlinear programming 문제가 된다.
\[\begin{align*} & \min 1 \\ s.t. \ & \frac{N_R}{N_S} \ge10\\ &N_S, N_P, N_R \ge 17 \\ & N_S, N_P. N_R \in Z^+ \\ & \frac{D_S}{N_S} = \frac{D_P}{N_P} = \frac{D_R}{N_R} = m\\ &D_R = D_S + 2D_P\\ & D_S \ge 8 \\ & D_R \le 130 \\ \end{align*}\]압력각 20도 기준 기어당 잇수가 17개 이상이어야 튼튼하다고 하여서 두 번째 조건을 추가하였고, 아래 두 조건은 각각 구동축 지름과 바퀴 지름을 고려한 조건이다.
이 문제는 해가 여러 개 존재할텐데, 손으로 풀어서 찾은 해는 다음과 같다.
\[(N_S, N_P, N_R, m) = (18, 99, 216, 0.6)\]이렇게 하면 기어비 12를 달성할 수 있다.
제작
Autodesk inventor를 이용해 stl 파일을 제작 후 3D 프린터로 인쇄하였다.
인벤터에서 기어를 쉽게 제작하는 방법을 소개하겠다.
1) 인벤터에서 새 조립품 문서를 생성한 후, 설계>전동>스퍼 기어 선택
2) 설계 안내서에서 자동으로 계산하고 싶은 값 선택(중심 거리로 하는게 편한듯)
3) 기어비 입력: 13처럼 넣어줘도 되는데, 잇수를 다 계산해놨으면 216/99처럼 입력해주는게 더 좋음
4) Ring gear처럼 내부 기어의 경우 내부 체크박스 선택
5) 모듈 값 입력
6) 기어1 드롭다운에 “구성요소” 선택
7) 이나비 칸에 기어 두께 입력
8) 기어2 드롭다운에 “모형 없음” 선택 → 1개의 기어만 생성됨
9) 계산 및 확인: 계산 실패 알림이 뜨면 무시하고 승인을 누른다.
10) 생성된 기어 우클릭 후 “톱니 쉐이프 내보내기” 선택 → 새 부품 파일이 생성됨
11) 사진과 같이 이 형상이 그려진 것을 확인할 수 있다.
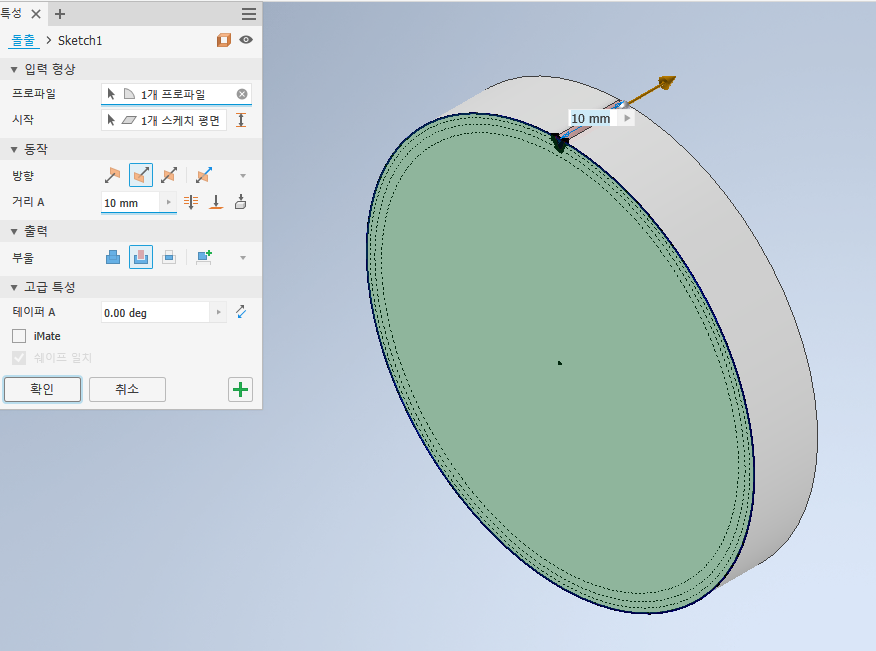
12) 돌출 컷을 해준다.
13) “원형” 기능을 이용하여 돌출을 회전축에 대해 잇수만큼 반복해준다.
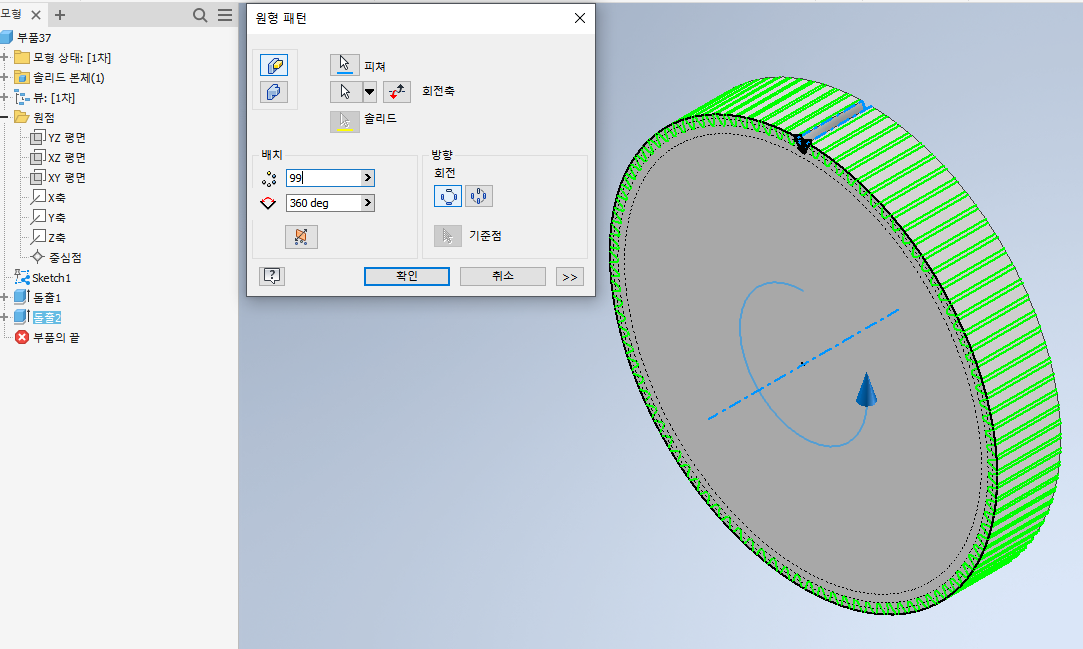
14) 완성!

반복해주면 이러한 유성 기어를 제작할 수 있다.
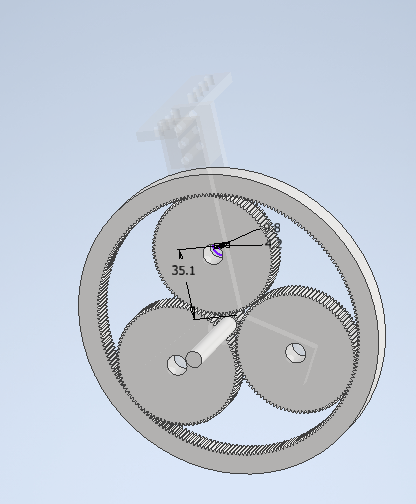
Planet gear의 회전축이 외부 구조물에 의해 고정되어 있기 때문에 sun gear를 돌리면 ring gear가 회전한다.