IMU

IMU는 관성 측정 장치를 뜻하는 Inertial Measurement Unit 약자이다. IMU는 주로 회전각(기울어짐)을 측정하기 위해 사용하는 장치이다.

구성

IMU에는 가속도계와 자이로스코프가 기본적으로 내장되고, 제품에 따라 지자기계가 추가된다. 가속도계와 자이로스코프만을 사용하면 6축 IMU, 지자기계까지 사용하면 9축 IMU가 된다.

가속도계는 특정 방향으로의 가속도를 측정하는 장치로, 세 개의 가속도계를 사용하면 3차원 가속도를 측정할 수 있다. 자이로스코프는 특정 방향으로의 각속도를 측정하는 장치로, 세 개의 자이로스코프를 사용하면 3차원 각속도를 측정할 수 있다.

IMU를 회전 측정 용도로 사용한다면 결국 3차원 정보만 얻게 되는 것인데, 이를 위해서 6개의 센서가 필요하다는 것이 약간은 이상할 수 있겠다. 하지만 실제로는 IMU가 6차원 정보를 갖고 있고, 이 중 우리가 원하는 3차원 정보만 추출하기 위해서는 6개의 센서가 필요하다고 이해하면 되겠다.

가속도계

가속도계를 이용해 회전을 측정하는 방법을 알아보자.

다음과 같은 spatial frame과 body frame을 고려하자. Spatial frame은 z축이 연직 방향으로 정렬된 좌표계이고, body frame은 현재 IMU 센서의 rotation을 나타낸다. 중력을 제외하고는 IMU에 가해지는 외력이 없다 가정한다면, IMU의 가속도 벡터는 \(\vec g_s = (0 \ 0 \ -g)^T\)가 될 것이다. 가속도 벡터를 \(\{ b \}\)에서 나타내면 \(\vec g _b = R_{bs} \vec g_s\)인데, 이것이 IMU에서 측정한 3차원 가속도 벡터가 될 것이다. 가속도계 정보로부터 \(\vec g_b\)를 알 수 있으므로, \(R_{bs}\)를 유추할 수 있다.

Rotation matrix \(R_{bs}\)를 구하기 위해 ZYX Euler angle을 고려하자. \((R, P, Y) = (\alpha, \beta, \gamma)\)를 가정하면

\[\begin{align*} R_{sb} & = R_z(\gamma) R_y(\beta) R_x(\alpha) \\ & = \begin{pmatrix} c_\gamma & -s_\gamma & 0 \\ s_\gamma & c_\gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} c_\beta & 0 & s_\beta \\ 0 & 1 & 0 \\ -s_\beta & 0 & c_\beta \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_\alpha & -s_\alpha \\ 0 & s_\alpha & c_\alpha \end{pmatrix} \\ & = \begin{pmatrix} c_\gamma & -s_\gamma & 0 \\ s_\gamma & c_\gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} c_\beta & s_\beta s_\alpha & s_\beta c_\alpha \\ 0 & c_\alpha & -s_\alpha \\ -s_\beta & c_\beta s_\alpha & c_\beta c_\alpha \end{pmatrix} \\ & = \begin{pmatrix} c_\gamma c_\beta & c_\gamma s_\beta s_\alpha - s_\gamma c_\alpha & c_\gamma s_\beta c_\alpha + s_\gamma s_\alpha \\ s_\gamma c_\beta & s_\gamma s_\beta s_\alpha + c_\gamma c_\alpha & s_\gamma s_\beta c_\alpha - c_\gamma s_\alpha \\ -s_\beta & c_\beta s_\alpha & c_\beta c_\alpha \end{pmatrix} \end{align*}\]

를 구할 수 있다.

\[\begin{align*} R_{bs} & = R_{sb}^T \\ & = \begin{pmatrix} c_\gamma c_\beta & c_\gamma s_\beta s_\alpha - s_\gamma c_\alpha & c_\gamma s_\beta c_\alpha + s_\gamma s_\alpha \\ s_\gamma c_\beta & s_\gamma s_\beta s_\alpha + c_\gamma c_\alpha & s_\gamma s_\beta c_\alpha - c_\gamma s_\alpha \\ -s_\beta & c_\beta s_\alpha & c_\beta c_\alpha \end{pmatrix} ^T \\ & = \begin{pmatrix} c_\gamma c_\beta & s_\gamma c_\beta & -s_\beta \\ c_\gamma s_\beta s_\alpha - s_\gamma c_\alpha & s_\gamma s_\beta s_\alpha + c_\gamma c_\alpha & c_\beta s_\alpha \\ c_\gamma s_\beta c_\alpha + s_\gamma s_\alpha & s_\gamma s_\beta c_\alpha - c_\gamma s_\alpha & c_\beta c_\alpha \end{pmatrix} \end{align*}\]

이때 \(\vec g_s\)의 \(x, y\) 성분이 0이므로 \(\vec g_b\)는 \(R_{bs}\)의 3열의 상수배가 나오게 된다.

\[\begin{align*} \vec g_b & = R_{bs} \vec g_s \\ & = R_{bs} \begin{pmatrix} 0 \\ 0 \\ -g \end{pmatrix} \\ & = r_3 (-g) \\ & = \begin{pmatrix} g s_\beta \\ -g s_\beta s_\alpha \\ -g c_\beta c_\alpha \end{pmatrix} \\ & = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} \end{align*}\]

따라서 다음의 식을 통해 \(\alpha, \beta\)를 구할 수 있다.

\[\begin{align*} \alpha & = \tan^{-1} \left( \frac{a_y}{a_z} \right) \\ \beta & = \tan^{-1} \left( \frac{a_x}{\sqrt{a_y^2 + a_z^2}} \right) \end{align*}\]

가속도계를 통해 자세를 측정하는 방법은 세 가지 문제에 직면한다.

중력 외의 외력이 작용할 경우 정확한 측정이 불가능 → 자이로스코프와 센서 퓨전
Yaw angle 측정 불가능 → 자이로스코프, 지자기계를 사용하여 측정
짐벌락, singularity? (ex. \(c_\beta = 0\)) → 쿼터니언 사용하여 해결

*쿼터니언 간단 설명

Quaternion은 수학자 William Hamilton이 발견한 개념으로, 허수단위 \(i\)처럼 동작하는 \(j,k\)의 개념을 추가하여 basis가 4개인 수 체계이다. 우리말로는 4원수라고 한다. 사원수에서는 우리가 사용하는 수 체계에 다음의 조건을 추가하여 사용한다.

\[i^2 = j^2 = k^2 = ijk = -i\]

Quaternion을 이용해 회전을 나타낼 수 있는데, 이는 rotation matrix 및 exponential coordinate의 개념과 꽤나 유사하다. \(\vec \omega = (\omega_x \ \omega_y \ \omega_z)^T\)에 대해 \(\theta\)만큼의 회전을 나타내기 위해서는 다음과 같은 quaternion \(q\)를 정의한다.

\[q = \cos\frac \theta 2 + i \omega_x\sin\frac\theta 2 + j \omega_y\sin\frac\theta 2 + k\omega_z\sin\frac\theta 2\]

이후 quaternion product \(\otimes\)를 다음과 같이 정의한다.

\[\begin{align*} \mathbf{a} \otimes \mathbf{b} & = [a_1 \ a_2 \ a_3 \ a_4 ] \otimes [b_1 \ b_2 \ b_3 \ b_4 ] \\ & = \begin{bmatrix} a_1b_1 - a_2b_2 - a_3b_3 - a_4b_4 \\ a_1b_2 + a_2b_1 + a_3b_4 - a_4b_3 \\ a_1b_3 - a_2b_4 + a_3b_1 + a_4b_2 \\ a_1b_4 + a_2b_3 - a_3b_2 + a_4b_1 \end{bmatrix} \end{align*}\]

Quaternion product는 \(i, j, k\)간의 곱셈을 떠올리면 쉽게 이해할 수 있다.

Quaternion을 이용한 회전 연산은 다음과 같이 계산할 수 있다.

\[v'= q \otimes v \times q^{-1}\]

이때 \(qq^*=1\)이므로 다음과 같이 쓸 수 있다.

\[v' = q \otimes v \otimes q^*\]

이는 마치 rotation matrix와 같은 작용을 하는데, 실제로 quaternion과 rotation 간의 일대일대응을 할 수 있다. 인터넷에 찾아보면 사람들이 다음의 식을 유도해 놓았다.

\[\mathbf{R}(q) = \begin{bmatrix} 2q_1^2 - 1 + 2q_2^2 & 2(q_2q_3+q_1q_4) & 2(q_2q_4 - q_1q_3) \\ 2(q_2q_3 - q_1q_4) & 2q_1^2 - 1 +2q_3^2 & 2(q_3q_4 + q_1q_2) \\ 2(q_2q_4 + q_1q_3) & 2(q_3q_4 - q_1q_2) & 2q_1^2-1+2q_4^2 \end{bmatrix}\]

다만 나는 조금 더 간단하게 생각할 수 있다고 생각한다. 두 가지 방법이 있는데, 서로 비슷하다.

1) Exponential coordinate

\(q\)와 \((\hat\omega,\theta)\)가 일대일대응인데 \(R\)도 \((\hat\omega,\theta)\)와 일대일대응이므로 관계식을 쉽게 찾을 수 있다.

2) \(i,j,k\)와 \(\hat x, \hat y, \hat z\)의 대응관계

\[R = \text{expm}(\lceil \hat\omega \rceil \theta) = \begin{pmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{pmatrix}\]

일 때, 다음의 식을 유도할 수 있다.

\[q \cdot i \cdot q^* = r_{11}i + r_{21}j + r_{31}k \\ q \cdot j \cdot q^* = r_{12}i + r_{22}j + r_{32}k \\ q \cdot k \cdot q^* = r_{13}i + r_{23}j + r_{33}k \\\]

그런데 우리는 다음의 식을 알고 있다.

\[R\hat x = r_{11}\hat x + r_{21}\hat y + r_{31}\hat z\\ R\hat y = r_{12}\hat x + r_{22}\hat y + r_{32}\hat z\\ R\hat z = r_{13}\hat x + r_{23}\hat y + r_{33}\hat z\]

두 식으로부터 모티브를 얻어서, \(q \otimes v \otimes q^*\)를 matrix form으로 바꿀 수 있을 것이라 생각하였고 결과는 다음과 같다.

\[\begin{pmatrix} q_1 & q_2 & q_3 & q_4 \\ q_1 & q_2 & q_3 & q_4 \\ q_1 & q_2 & q_3 & q_4 \\ q_1 & q_2 & q_3 & q_4 \\ \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & v_x & 0 & 0 \\ 0 & 0 & v_y & 0 \\ 0 & 0 & 0 & v_z \end{pmatrix} \begin{pmatrix} q_1 & q_1 & q_1 & q_1 \\ q_2 & q_2 & q_2 & q_2 \\ q_3 & q_3 & q_3 & q_3 \\ q_4 & q_4 & q_4 & q_4 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & R \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & v & v & v \end{pmatrix}\]

조금 더 깔끔하게 정리할 수 있을 것 같은데, 그건 나중에 하자!

자이로스코프

자이로 센서를 이용해 회전을 측정하는 방법을 알아보자.

자이로 센서를 이용하면 세 방향으로의 각속도를 측정할 수 있다. 각속도를 알고 있으므로, 이를 적분하여 각변위를 구할 수 있다.

\[\begin{align*} \alpha & = \int \omega_x dt \\ \beta & = \int \omega_y dt \\ \gamma & = \int \omega_z dt \end{align*}\]

(각속도 벡터가 body frame에서 나타나 있으니까 이것을 spatial frame에서 다시 나타낸 후 적분해야 하는 것 아닌가?)

자이로 센서를 통해 자세를 측정하는 방법은 두 가지 문제에 직면한다.

초기 각변위를 알 수 없음 → 0으로 가정 / 보정 / 가속도계와 센서 퓨전
적분 오차가 누적되면 long-term 오차 발생 → 가속도계 및 지자기계와 센서 퓨전

지자기계

지자기 센서는 자기장의 세기를 측정하는 센서이다. 지구는 거대한 자석이기 때문에, IMU가 북쪽 방향으로 정렬되어 지구의 자기력선과 일치할 때 지자기 센서가 최대값을 측정한다. 따라서 지자기계를 사용하면 yaw 값을 측정할 수 있다.

지자기계를 통해 자세를 측정하는 방법은 세 가지 문제에 직면한다.

Roll, pitch 값을 알 수 없음 → 가속도계, 자이로스코프를 통해 측정
주변 전기장/자기장에 영항을 받음 → 어쩔 수 없음/보정 필요
진북과 자북이 다름 → 위도 정보를 알고 있다면 편각(declination)을 알 수 있으므로 보정 가능

필터

가속도계를 이용한 자세 추정은 중력가속도가 아닌 다른 가속도로 인해 short-term 오차가 발생하고, 자이로 센서를 이용한 자세 추정은 적분 오차로 인한 long-term 오차가 발생하므로 이것을 적절하게 조합하면 오차를 줄일 수 있다는 개념이 바로 센서 퓨전이다.

아래 세 개의 필터는 센서 퓨전을 위한 대표적인 알고리즘이다.

Complementary filter (상보 필터)

상보 필터의 식부터 보면 다음과 같다. 자이로 센서를 통해 측정한 각속도를 \(\dot\theta_g\), 가속도계를 통해 측정한 각도를 \(\theta_a\)라 하면 상보 필터를 통해 추정하는 각도는

\[\theta_c \leftarrow \alpha\theta_c +\dot\theta_g \Delta t + (1-\alpha)\theta_a, \ \alpha = 1 - \tau \Delta t\]

로 나타낼 수 있다. 이때 \(\Delta t\)는 센서들의 sampling time이고 \(\tau\)는 적당한 상수값이다.

이 필터가 어떻게 잘 동작할 수 있는지 이해하기 위해서는 LPF와 HPF에 대한 간단한 이해가 필요하다. LPF는 저주파 성분만 통과시키는 필터이고, HPF는 고주파 성분만 통과시키는 필터이다. 이를 시간 영역에서 해석해보면 LPF를 적용하면 long term 신호만 통과하고 HPF를 적용하면 short term 신호만 통과한다. 가속도계의 신호는 short term 오차가 있으므로 LPF를 적용하여 long term 신호만 사용하고, 자이로 센서의 신호는 long term 오차가 있으므로 HPF를 적용하여 short term 신호만 사용하자.

1차 LPF와 HPF의 전달함수는 다음과 같이 나타낼 수 있다.

\[\begin{align*} LPF(s) & = \frac{\tau}{s+\tau} \\ HPF(s) & = \frac{s}{s+\tau} \end{align*}\]

이때 \(\tau\)는 cutoff frequency이다.

\[\begin{align*} \theta_c(s) & = HPF(s)\theta_g(s) + LPF(s)\theta_a(s) \\ & = \frac{s}{s+\tau} \frac 1 s \omega_g(s) + \frac{\tau}{s+\tau}\theta_a(s) \\ & = \frac{1}{s+\tau}\omega_g(s) +\frac{\tau}{s+\tau}\theta_a(s) \\ (s+\tau)\theta_c(s) & = \omega_g(s) + \tau\theta_a(s) \\ \dot \theta_c(t) + \tau\theta_c(t) & = \omega_g(t) + \tau\theta_a(t) \\ \end{align*}\]

마지막 식을 이산 시간 영역으로 옮겨와 정리하면,

\[\begin{align*} \frac{\theta_{c, k+1} - \theta_{c,k}}{\Delta t} + \tau\theta_{c,k} & = \omega_{g,k} + \tau\theta_{a,k} \\ \theta_{c,k+1} & = (1-\tau\Delta t)\theta_{c,k} + \omega_{g,k} \Delta t + \tau\Delta t\theta_{a,k} \\ \theta_{c,k+1} & = \alpha \theta_{c,k} + \omega_{g,k} \Delta t + (1-\alpha)\theta_{a,k} \\ \end{align*}\]

를 구할 수 있다.

(다른 버전)

혹자는

\[\theta_c = \alpha \theta_g + (1-\alpha)\theta_a, \ \alpha = \frac{\tau}{\tau+\Delta t}\]

를 사용하기도 한다. 이것도 잠시 살펴보면

\[LPF(s) X(s) = \bar X(s)\]

라 하면, 위와 비슷한 방법으로

\[\bar x _k = \frac{\tau}{\tau + \Delta t}\bar x _{k-1} + \frac{\Delta t}{\tau+\Delta t}x_k\]

를 구할 수 있다.

HPF도 비슷하게

\[\bar y_k = \frac{\tau}{\tau + \Delta t}(\bar y_{k-1} + y_k - y_{k-1})\]

로 쓸 수 있다. 이때 이전 timestep의 값을 쓰지 않고 현재 timestep의 값만 사용한다고 생각하면

\[\begin{align*} \bar x_k & = \frac{\Delta t}{\tau + \Delta t}x_k \\ \bar y_k & = \frac{\tau}{\tau + \Delta t} y_k \end{align*}\]

이므로 \(\theta_c = \bar \theta_g + \bar \theta_a\)로 쓰고 \(\bar \theta_g = \theta_c + \dot\theta_g \Delta t\)로 쓰면

\[\theta_c \leftarrow \alpha (\theta_c + \omega_g \Delta t) + (1-\alpha)\theta_a\]

로 구할 수 있다.

뭐가 더 좋을지는 잘 모르겠다.

Kalman filter (칼만 필터)

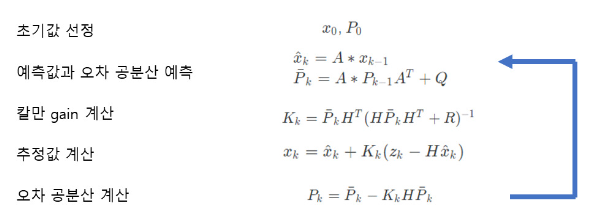
Untitled

이 부분은 칼만 필터 공부 후 다시 작성할 예정

Madgwick filter (매드그윅 필터)

Madgwick filter도 complementary filter와 비슷한 형태인데, 조금 더 복잡하다.

Madgwick filter의 유도는 다음의 식을 어떻게 더 잘 쓸 수 있을까라는 고민을 해결하는 과정이다.

\[q_{\text{est},t} = \gamma_t q_{\text{acc}, t} + (1-\gamma_t)q_{\text{gyro},t}\]

(1) \(q_{\text{acc}, t}\)를 어떻게 계산할 것인가

(2) \(q_{\text{gyro},t}\)를 어떻게 계산할 것인가

(3) Weight \(\gamma_t\)를 어떻게 설정할 것인가

(1) \(q_{\text{acc}, t}\)를 어떻게 계산할 것인가

Accelerometer 측정 결과를 이용해 자세를 추정하는 방법으로, Madgwick에서는 optimization을 사용하였다. 위에서 설명한 방법과 거의 동일하지만, analytic하게 풀지 않고 optimization을 쓰는 이유는 quaternion을 complete하게 구하기 위해서이다. 위에서 설명한 방법에서는 yaw를 알 수 없었기 때문에 quaternion 또한 unique, complete하게 계산되지 않는다. 대신 optimization을 쓰면 하나의 quaternion을 구할 수 있다. Formulation은 다음과 같다.

\[\underset{\hat q}{\text{argmin }} \hat q^{-1} \otimes \hat g \otimes \hat q - \hat s\]

이때 \(\hat q\)는 spatial frame에 대한 IMU의 자세, \(\hat g\)는 gravity acceleration, \(\hat s\)는 가속도계를 통해 측정한 가속도 벡터이다.

이 최적화 문제는 gradient descent를 통해 풀 수 있는데, 이때 gradient를 jacobian을 이용해 analytic하게 구했기 때문에 속도가 빠르다는 것이 Madgwick의 주장이다.

Update rule은 아래와 같다.

\[q_{k+1} = \hat q_k - \mu \frac{\nabla f}{||\nabla f||}, \nabla f = J^T f\\ \mu_t = \alpha ||\dot q||\]

Analytic jacobian을 계산하는 과정은 원문을 참고.

(2) \(q_{\text{gyro},t}\)를 어떻게 계산할 것인가

다음의 공식을 이용한다.

\[\mathbf{\omega} = [0 \ \omega_x \ \omega_y \ \omega_z] \\ \dot q = \frac 1 2 \hat q \otimes \mathbf{\omega}\]

이를 이용하면 update rule은

\[\dot q _t = \frac 1 2 \hat q_{\text{est}, t-1} \otimes \omega_t \\ q_{\omega, t} = \hat q_{\text{est}, t-1} + \dot q_{\omega, t} \Delta t\]

(3) Weight \(\gamma_t\)를 어떻게 설정할 것인가

여기서도 재미있는 트릭이 나온다. Madgwick 씨는 \(\gamma_t\)의 optimal value가 \(q_\text{acc}\)의 weighted convergence와 \(q_\text{gyro}\)의 weighted divergence가 같아지게 하는 값이라고 주장하고, 다음과 같이 계산하였다.

\[(1-\gamma_t)\beta = \gamma_t \frac{\mu_t}{\Delta t} \\ \gamma_t = \frac{\beta}{\frac{\mu_t}{\Delta t}+\beta}\]

이때 \(\beta\)가 filter gain으로써 tuning parameter가 되는 듯하다.

Gradient descent를 할 때 사용하는 \(\alpha\)를 매우 크게 설정하면 \(\mu_t\)가 매우 큰 값이 되므로 다음의 두 근사가 유효하다.

\[q_\text{acc} \approx -\mu_t \frac{\nabla f}{||\nabla f||} \\ \gamma_t \approx \frac{\beta \Delta t}{\mu_t}\]

이 근사를 적용하면

\[q_{\text{est},t} = \hat q _{\text{est}, t-1} + \dot q _{\text{est},t}\Delta t \\ \dot q_{\text{est}, t} = \dot q_{\text{gyro}, t} - \beta \dot{\hat q}_{\epsilon, t}\\ \dot{\hat q}_{\epsilon, t} = \frac{\nabla f}{||\nabla f||}\]

로 필터가 단순해진다.

필터의 다이어그램은 아래와 같다.

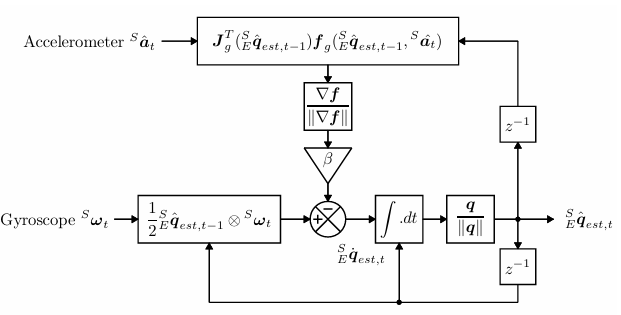
Untitled